Богдан Кравцов

Анализ игры «Словль»

Правила игры

В игре «Wordle» и в её русскоязычной реплике «Словль» требуется максимум за шесть попыток отгадать пятибуквенное слово — секрет.

Игрок ходит словом из пяти букв, а ведущий сравнивает это слово с секретом и красит в попытке зелёным цветом те буквы, которые в обоих словах стоят на одних и тех же местах, а жёлтым — совпадающие буквы, стоящие на разных местах.

Например, при секрете ЗНАМЯ попытка ЗАКОН будет раскрашена так: ЗАКОН. Наравне с цветовой нотацией я использую символьную, в которой эта же раскраска записывается так:


Если и в попытке, и в секрете по два раза встречается одна и та же буква, то она будет покрашена дважды.

Как и во многих других играх со словами, в качестве секретов и попыток в «Словле» используются только имена существительные в именительном падеже, а буквы Ё и Е не различаются.

Эта игра похожа на игру «Быки и коровы». В словесной разновидности «Быков и коров» секретами и попытками могут быть только слова, в которых все буквы разные, и ведущий не сообщает, какие именно буквы совпали, а лишь называет количество «быков» и «коров». Быки — совпадения букв, стоящих на одинаковых местах, а коровы — совпадения букв, стоящих на разных местах.

В обеих играх совпадения букв симметричны относительно замены попытки на секрет. Так, слова ПОЛЮС и САЛЮТ — это два быка и одна корова, с какой стороны ни посмотри.

Тех, кто хочет во всём разобраться сам, предупреждаю: дальше я буду конструировать стратегии, в статье будут спойлеры.

Разведка, пристрелка, атака

В каждом раунде игры я выделяю три стадии — разведка, пристрелка и атака.

В разведке у меня нет цели на каждом шагу отгадать секрет. Я перебираю как можно больше разных букв, чтобы как можно больше узнать про секрет и как можно строже ограничить множество возможных секретов.

В атаке я хожу только словами, которые строго удовлетворяют всем найденным ограничениям, и при этом стараюсь занять наиболее частые буквы из новых.

Я перехожу от разведки к атаке, когда допустимых секретов осталось настолько мало, что я с трудом подбираю хотя бы один вариант. Если и ограничений много, и вариантов больше двух, мне нужна пристрелка, которая за один ход отбирает из этих гипотез верную.

Успех в атаке зависит от способности игрока вспомнить слова, подходящие под уже известные ограничения. Этот навык тренируется в разных играх со словами. И чем увереннее вы чувствуете себя в атаке, тем короче вам нужна разведка.

Игровой словарь

Поскольку у меня нет списка слов, допустимых в игре, в качестве игрового словаря я выбрал все пятибуквенные существительные из Грамматического словаря.

Всего в ГС 3646 подходящих слов.

Для статистических целей подошла бы и выборка из размеченного корпуса текстов, то есть такого, в котором прописаны части речи и грамматические характеристики всех слов. Например, из Национального корпуса русского языка.

Частотность букв

Я исхожу из предположения, что все слова из словаря загадываются с равной вероятностью, поэтому частотность слов в реальных текстах мне не нужна. Мой анализ строится на том, как часто и на каких местах разные буквы встречаются в словах из словаря:

Буква	На всех местах	Первая	Вторая	Третья	Четвёртая	Пятая
А	2242	127	750	171	362	832
О	1551	204	552	132	519	144
К	1256	317	76	142	341	380
Р	1170	160	229	408	153	220
Е	1079	13	418	168	397	83
И	1046	62	332	144	382	126
Т	957	195	125	256	126	255
Л	886	150	136	335	157	108
Н	862	130	59	222	190	261
С	818	334	59	177	93	155
У	652	59	349	70	169	5
П	596	316	57	147	35	41
М	562	203	47	173	74	65
В	496	191	62	128	64	51
Б	486	214	62	133	44	33
Д	462	147	21	138	69	87
З	363	112	41	107	52	51
Г	360	143	28	93	49	47
Я	279	22	36	27	47	147
Ш	278	130	7	75	31	35
Ь	250	0	8	3	68	171
Ы	244	0	104	28	46	66
Ч	224	72	8	82	26	36
Х	211	82	13	52	24	40
Ф	193	108	9	43	16	17
Ж	188	56	8	68	28	28
Ц	181	37	4	28	37	75
Й	157	3	6	57	9	82
Ю	89	11	30	21	24	3
Щ	48	19	4	11	14	0
Э	39	29	4	4	0	2
Ъ	5	0	2	3	0	0

Частоты букв в игровом словаре отличаются от частот букв в реальных текстах. Вот два частотных рейтинга:


В первой строке буквы отсортированы по убыванию их частот в игровом словаре, во второй — по убыванию их частот в реальных текстах, на материале Национального корпуса русского языка из Нового словаря частотности.

Хинт: самые частые буквы расположены, как правило, в середине клавиатуры, под указательными пальцами.

Повторы букв

Буквы повторяются в 30% слов (1093 из 3646).

Два мягких знака есть только в одном слове: ПЬЯНЬ. А чаще других букв повторяется А: две или три А встречаются в 379 словах; это чаще, чем в каждом десятом слове.

Но даже вторая А встречается реже, чем шестнадцатая в рейтинге буква Д, поэтому начинать игру выгоднее словами, в которых все буквы разные и при этом наиболее частые, — так я зацеплю больше возможных секретов. А о повторах нужно вспомнить в атаке.

Гласные

Две гласных буквы в 3021 слове, это 83% словаря. Всего одна гласная буква в 348 словах, три — в 277. Слов без гласных и слов с четырьмя или пятью гласными в игровом словаре нет.

Исходя из этого, пока я знаю одну гласную букву из секрета или ни одной, мне выгодно искать ещё одну гласную, то есть играть словами с тремя и двумя гласными, а когда узнал вторую — больше внимания уделять согласным, то есть ходить словами с одной новой гласной.

Если я перебрал А, О, Е, И, У и нашёл только одну гласную, и это А или О, то разумно проверить вторую такую же:

Сочетания	А	О
Одна А или О	85	66
× 2 или × 3	379	206
+ Ы, Э, Ю или Я	230	157

К-число и Б-число

Все буквы разные в 2553 словах.

Для каждого из них я посчитал два числа — сумму общих частот всех пяти букв, К-число, и сумму частот пяти букв на своих же местах, Б-число. Вот пример расчёта для слова БОНУС:

Буква	Σ	Б	О	Н	У	С
О	1551	204	552	132	519	144
Н	862	130	59	222	190	261
С	818	334	59	177	93	155
У	652	59	349	70	169	5
Б	486	214	62	133	44	33

Теперь я составлю КБ-рейтинг слов, отсортировав их в первую очередь по убыванию К-чисел, а при равенстве — по убыванию Б-чисел.



Самый низкий КБ-рейтинг — у слова УЗДЦЫ:

Алгоритм «Норка»

Этот алгоритм построен на слове с самым высоким КБ-рейтингом — НОРКА.

Первый ход этим словом максимизирует количество совпадений букв на множестве всех слов из словаря. После него в 29,6% секретов (1081 из 3646) будут известны как минимум три буквы.

Если совпадений недостаточно для атаки, я хожу словами с высоким КБ-рейтингом и без буквенных пересечений со словом НОРКА. В зависимости от числа гласных, покрашенных в первой попытке, следующим ходом будет слово либо с двумя гласными (МЕТИЛ, СЕМИТ, МЕТИС, БИЛЕТ), либо с одной (ГЛИСТ, ЛЕСТЬ, СТИЛЬ).

После этого как минимум три буквы будут известны у 77,7% секретов (2832 из 3646).

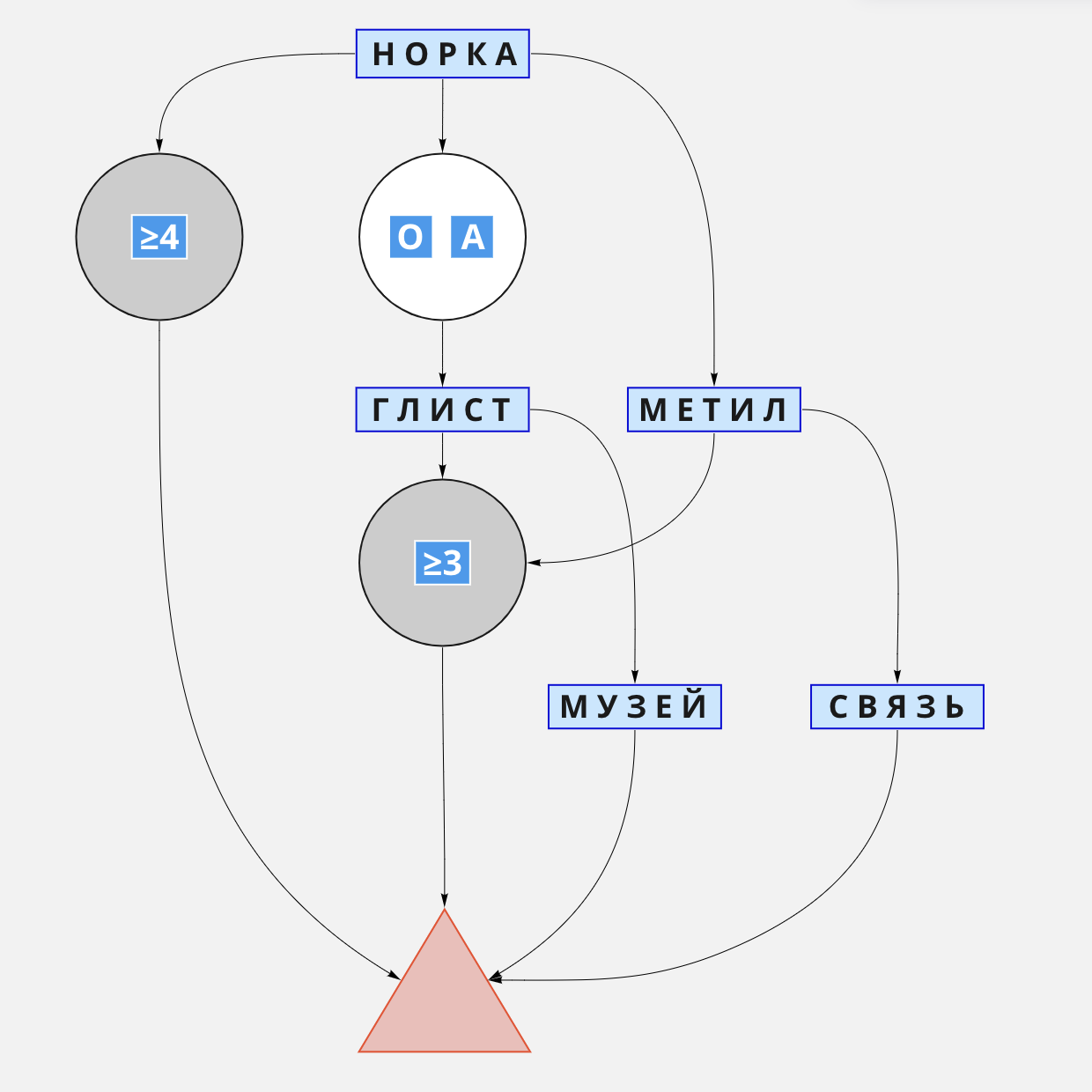
После двух ходов НОРКА и ГЛИСТ, если совпадений недостаточно, я продолжаю разведку словом МУЗЕЙ.


Визуализированный алгоритм «Норка»:

Десять букв

Из десяти наиболее частых букв, А, О, К, Р, Е, И, Т, Л, Н, С, можно сложить 52 пары слов. Они будут панграммами на усёченном наборе букв и ограниченном множестве слов.

Сумма К-чисел двух слов, КΣ, у всех пар одинакова, 11 867. Это значит, что за два хода о наборе (но не о местах) букв секрета они дадут одну и ту же информацию.

Эти пары различаются по двум другим параметрам: Б-числу пары (БΣ) и К-числу первого слова из пары (К1). Чем больше К1, тем больше я буду знать о наборе букв секрета уже после первого хода. Чем больше БΣ, тем больше будет информации о местах букв в секрете после второго хода.

Вот несколько таких пар. В каждой паре на первом месте стоит слово с бо́льшим К-числом:

Алгоритм «Серна»

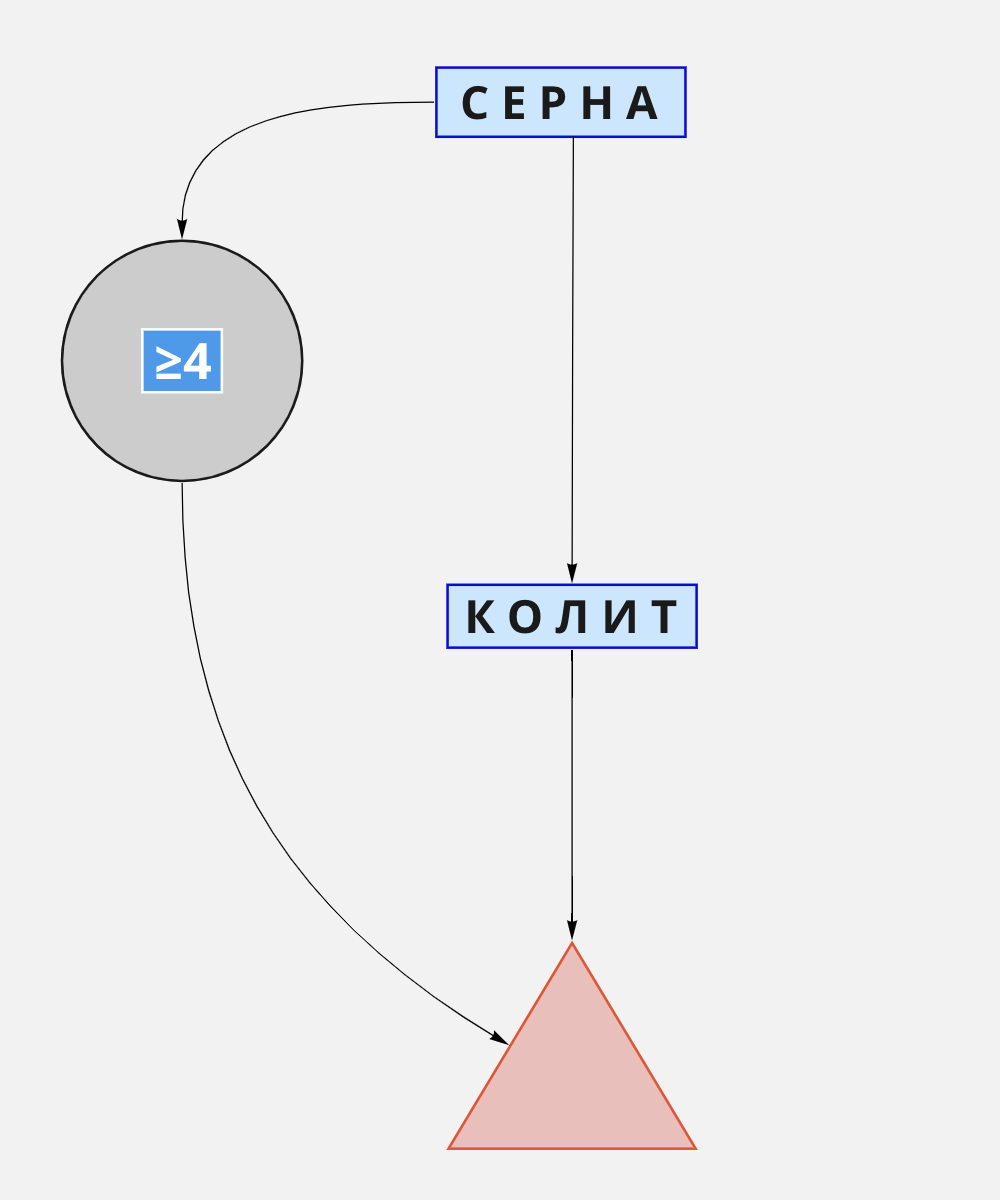
Этот алгоритм предлагает первые два хода сделать парой с максимальным КΣ. Я выбираю из них пару с наибольшим БΣ: СЕРНА + КОЛИТ.

После этих двух ходов как минимум три буквы будут известны для 79,6% секретов (2902 из 3646). Это немного больше, чем в алгоритме «Норка».

Как и в «Норке», совсем не будет совпадений с четырьмя словами: УЗДЦЫ, ВЗМЫВ, ЖМУДЬ＊, ЗУМПФ＊.

Визуализированный алгоритм «Серна»:

15, 20, 25, 30

Для игры в «Словль» это уже излишне, но пригодится в «Быках и коровах».

Из 15 самых частых букв можно составить 159 троек слов.
Из 20 самых частых букв можно составить 138 четвёрок слов.
Из 25 самых частых букв можно составить 37 пятёрок слов.

Вот примеры таких наборов и их БΣ. В первой строке блока — максимальный по БΣ набор. В каждой строке слова упорядочены по убыванию К-чисел:


После пяти ходов, сделанных любой из панграмм последнего блока, мне будут известны все буквы всех слов, кроме тех 44, в которых есть Ъ или Э. Одновременно эти две буквы ни в одном слове из игрового словаря не встречаются.

Для тридцати самых частых букв, то есть всех, кроме Ъ или Э, мне не удалось составить панграмму из шести пятибуквенных существительных.

Алгоритм «Опека»

Этот алгоритм уделяет больше внимания гласным, чем предыдущие.

Вот десять слов с наибольшим К-числом, в которых три гласных:


Я делаю первый ход тем из них, у которого максимальное Б-число, ОПЕКА, и дальше действую исходя из набора совпадений.

Три гласных совпали

Семь секретов, два из них уникальны по набору совпадений, три разбираются пристрелкой ДОГМА:

Два быка на гласных

— О и А. Cемь секретов, пристрелка ФИНАЛ приводит к победе на третьем ходу:

— О и Е. Восемь секретов, два из них уникальны по совпадениям согласных. Пристрелка ОЛЕНЬ, если это не секрет, приводит к победе на третьем ходу.

— Е и А. Сорок пять секретов. Если совпали согласные, я атакую, если нет, то хожу словом СТРУГ＊.

Бык и корова или две коровы на гласных

Если две согласные совпали, я атакую. Если одна или ни одной, то вторым ходом проверяю наиболее вероятные из новых согласных и пробую из гласной коровы сделать быка. Для каждого из этих вариантов я пересчитал частоты, включив в подсловарь только те слова, которые удовлетворяют всем ограничениям.

Одна гласная совпала или ни одной

На втором ходу продолжаю искать гласные словом РУБИН.

— Если после второго хода неизвестна ни одна гласная, продолжаю разведку словами ЯСТЫК＊ или ЛЫЖНЯ.

— Если одно или два совпадения, хожу словами ХЛЫСТ, МЫСЛЬ или СВЯЗЬ.

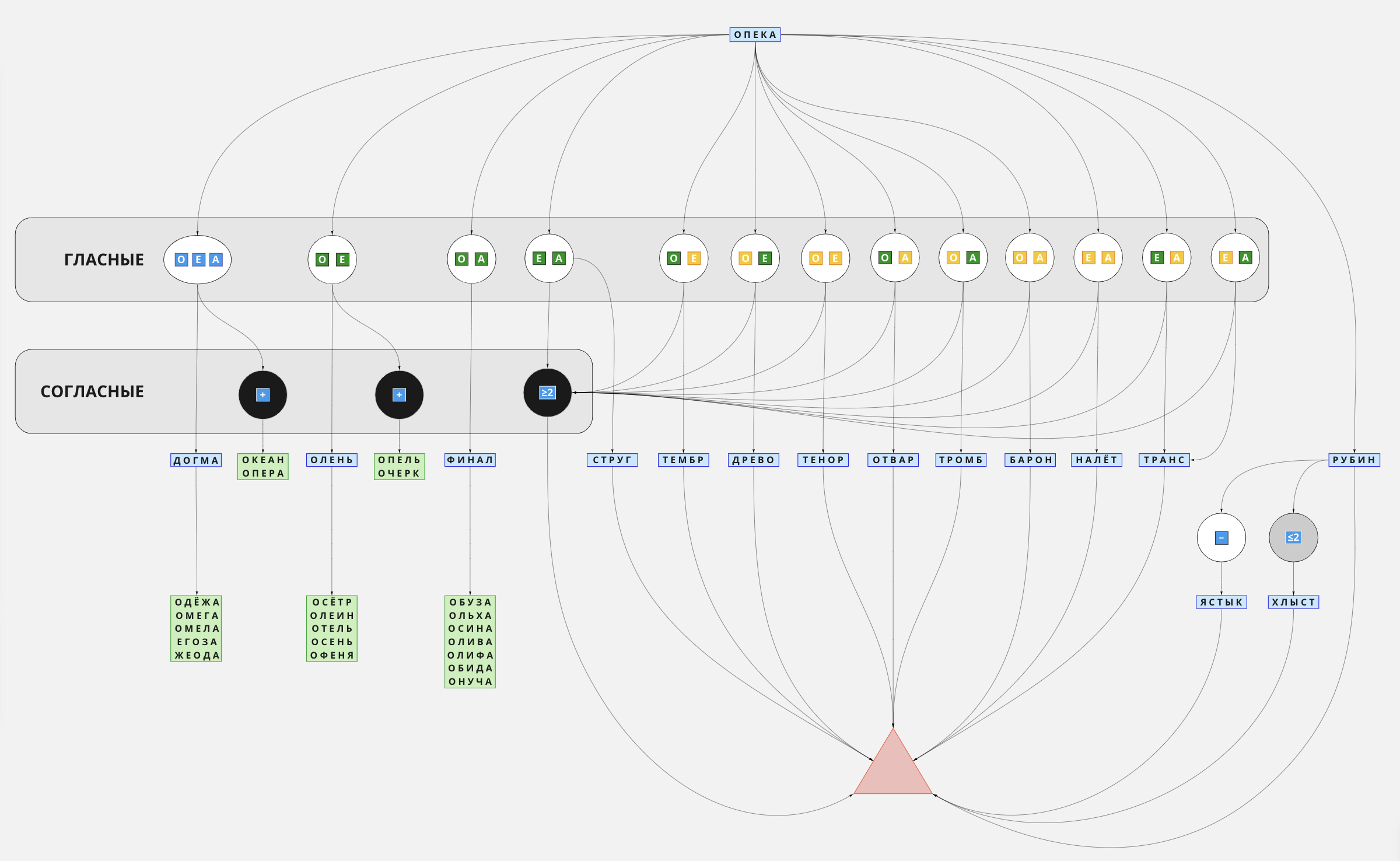
— Во всех остальных случаях атакую.

Визуализированный алгоритм «Опека»:

Тестирование алгоритмов

Чтобы сравнить практическую эффективность четырёх частотных алгоритмов, я сыграл по 110 раундов каждым из них:

— НОРКА, но со словом МЕТИС на втором ходу вместо слова МЕТИЛ;

— ОПЕКА;

— СЕРНА + КОЛИТ;

— СТЕНА + РОЛИК — другая панграмма десяти букв, с меньшими К1 и БΣ.

Результаты тестов в таблице:

Ходы	Норка	Опека	Серна	Стена
2	6	1	4	2
3	51	39	62	53
4	39	49	38	47
5	11	17	6	7
6	3	4	0	1
Среднее	3,582	3,855	3,418	3,564

И на графике:

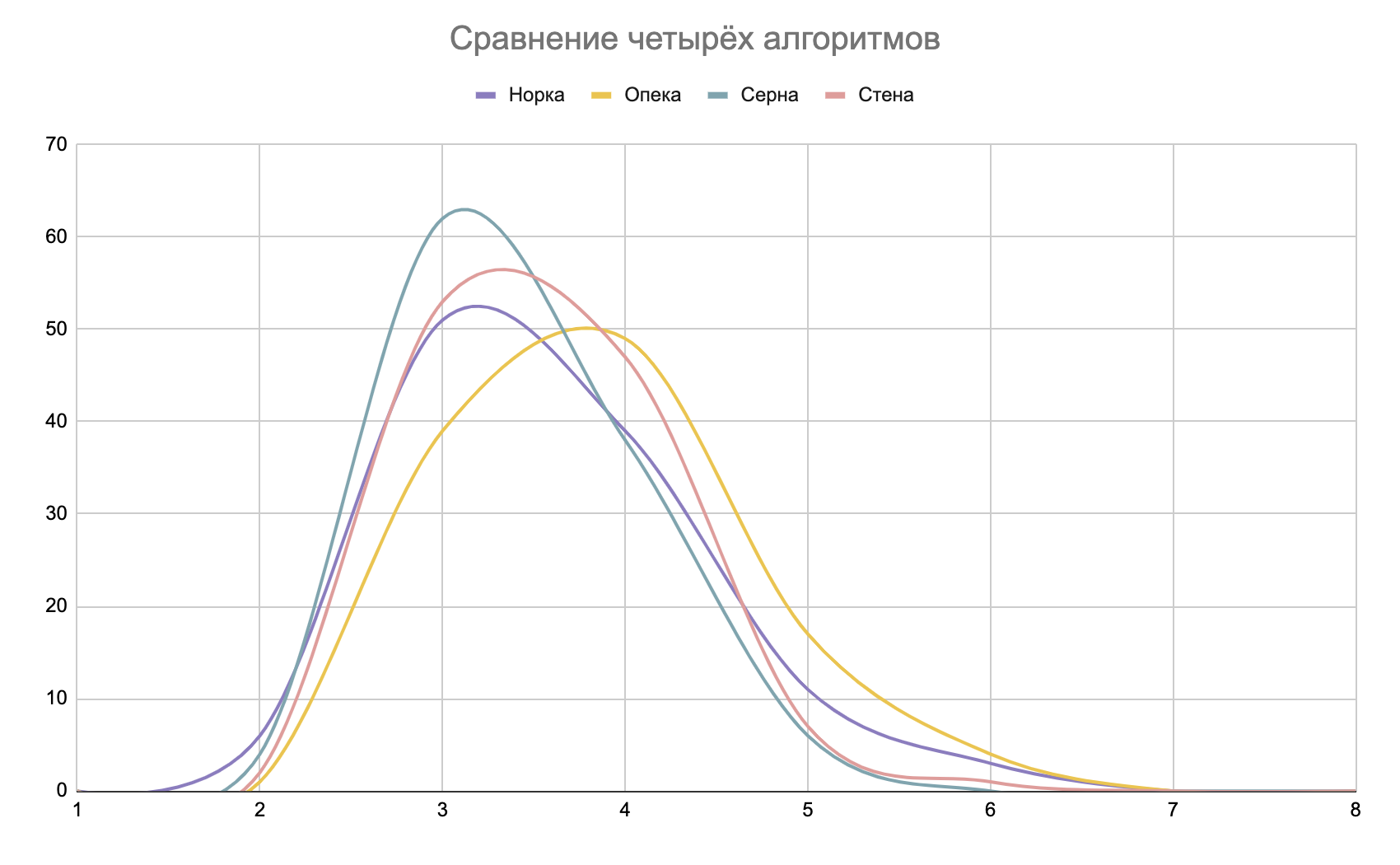
В моём случае «Серна» — лучшая по среднему числу ходов, «Стена» заметно проигрывает «Серне», «Норка» отгадывает больше всего секретов на втором ходу, но отстаёт на следующих, а «Опека» слабее трёх других.

У других игроков может получиться другое распределение эффективности, поэтому я буду благодарен тем, кто пришлёт мне результаты своего тестирования.

В одном раунде я угадал секрет с первой же попытки. Этот раунд я вычеркнул из результатов эксперимента и в следующих алгоритмах тоже буду вычёркивать.

Вот все мои игры: Норка, Опека, Серна, Стена.

Теория информации

Грант Сандерсон разобрал «Wordle» с точки зрения теории информации. Я повторю несколько шагов этого анализа со «Словлем» и сравню с результатами подхода, основанного на частоте букв.

В общих словах

В каждом раунде мне нужно правильно выбрать одно из 3646 слов, секрет. Для этого я задаю вопросы (это мои попытки), а от ведущего получаю в ответ информацию (раскраску), которая сокращает множество гипотез. Когда я слышу «пять быков» или вижу пять зелёных букв — ура, я исключил все неправильные слова.

Выгоднее ходить так, чтобы выяснить максимум новой информации и вычеркнуть как можно больше вариантов. Но я получаю информацию не тогда, когда называю слово, а когда узнаю его раскраску. То есть я не могу точно предсказать, сколько информации принесёт мне тот или иной ход, — это зависит от ответа.

Но я могу подсчитать ожидаемую информативность Ĩ своей попытки — среднее количество информации, которое я получу, считая все оставшиеся допустимые слова равновероятными. Каждому потенциальному секрету соответствует какая-то одна раскраска моей попытки. И если моя попытка будет покрашена именно так, то я смогу отсечь все слова, которые отвечают другим раскраскам.

В формулах

Количество информации измеряется в битах. Один бит информации нужен для того, чтобы выбрать единственный правильный вариант из двух равновероятных возможных.

Перед началом раунда для выбора правильного варианта из 3646 слов мне нужно выяснить U₀ = log₂3646 ≈ 11,832 битов информации. А если, скажем, после моего третьего хода осталось 490 вариантов, то мне нужно выяснить U₃ = log₂490 ≈ 8,937 битов. То есть фактическая информативность этих трёх ходов:

I_1-3 = log₂ ≈ 1,324

Чтобы вычислить ожидаемую информативность хода, понадобится разделить все оставшиеся допустимые слова по раскраскам, которым они соответствуют. Например, если все M оставшихся возможных секретов раскрашивают мою попытку тремя разными способами: M₁ слов одной раскраской, M₂ слов — второй и M₃ — третьей, то ожидаемая информативность попытки вычисляется по формуле:

Ĩ =

В общем виде:

Ĩ =

Возможны максимум 3⁵ = 243 раскраски одного слова, и чем равномернее по этим раскраскам распределяются возможные секреты, тем выше ожидаемая информативность хода. А если попытка будет покрашена одним и тем же способом при любом оставшемся секрете, то ожидаемая информативность такого хода будет нулевой. Такое случается, если сходить словом, составленным только из тех букв, про которые уже известно, что их нет в секрете.

Наибольшая ожидаемая информативность

Вот топ-20 слов с наибольшей ожидаемой информативностью в качестве первого хода:

Я выделил жёлтым те слова, которые попали и в топ-20 по убыванию КБ-рейтинга. Здесь таких одиннадцать.


Вот топ-10 пар слов с наибольшей ожидаемой информативностью в качестве неизменных первых двух ходов. На первом месте в каждой паре стоит слово с бо́льшей собственной ожидаемой информативностью в качестве первого хода.


На вершине этого списка стоит пара слов с максимальными КΣ и БΣ, СЕРНА + КОЛИТ.

«Коран» — жадный рекурсивный алгоритм

Жадный рекурсивный алгоритм предлагает каждый ход делать тем словом из оставшихся допустимых, которое как можно сильнее сокращает число гипотез в среднем. Например, если после третьего хода осталось 490 возможных секретов, этот алгоритм для четвёртого хода выбирает из них слово с наибольшей ожидаемой информативностью на этих же 490 словах.

Первый ход — слово КОРАН, поскольку у него максимальная ожидаемая информативность на списке из 3646 слов. Этому алгоритму требуется в среднем ~3,762 хода на то, чтобы разгадать секрет (при подсчёте этого числа, как и ранее, я исключил раунд, в котором секрет угадывается на первом ходу).

А вот все слова, которые КОРАН гарантированно отгадывает вторым ходом:

«Блажь» — жадный рекурсивный алгоритм с пристрелкой

Алгоритм «Коран» не предполагает пристрелки и из-за этого не успевает отгадать за шесть ходов 32 слова.

Например, после двух ходов КОРАН + СЕМИТ в списке допустимых секретов может остаться пять слов, которые жадный рекурсивный алгоритм не успевает перебрать за четыре оставшихся попытки:


В таких ситуациях и нужна пристрелка. Здесь она гарантирует победу даже не за шесть, а за пять попыток:


Алгоритм «Блажь» на каждом ходу выбирает слово с максимальной информативностью на оставшихся допустимыми секретах, но не только среди них, а вообще из всех 3646 слов. Этому алгоритму требуется в среднем ~3,655 хода, чтобы отгадать секрет. В 262 случаях он предлагает пристрелку.

Алгоритм «Колит»

Алгоритм «Блажь» не учитывает, что у пристрелки есть минус: при одинаковой ожидаемой информативности ход одной из N оставшихся гипотез с вероятностью 1/N приводит к победе на том же ходу, а пристрелка в любом случае не заканчивает игру сразу же. То есть по сравнению с пристрелкой атака имеет фору в 1/N оставшегося среднего количества ходов.

Этот алгоритм учитывает фору и оптимизирует не ожидаемую информативность, а ожидаемое количество ходов. Для самого информативного начала, КОРАН, эта поправка сократила среднее число ходов всего на 0,000823.

А вот первый ход словом КОЛИТ приводит к наименьшему среднему числу ходов, ~3,640.

Это сорок второе по информативности слово и четыреста девяносто третье — в списке всех слов по убыванию КБ-рейтинга.

Сравнение алгоритмов

Вот сравнение трёх информативных алгоритмов в таблице:

Ходы	Коран	Блажь	Колит
2	155	75	63
3	1302	1387	1460
4	1611	1912	1856
5	448	263	258
6	97	8	8
7	25	0	0
8	7	0	0
Среднее	3,762	3,655	3,640

На графике я нормировал вертикальную ось для согласования со сравнением частотных алгоритмов:

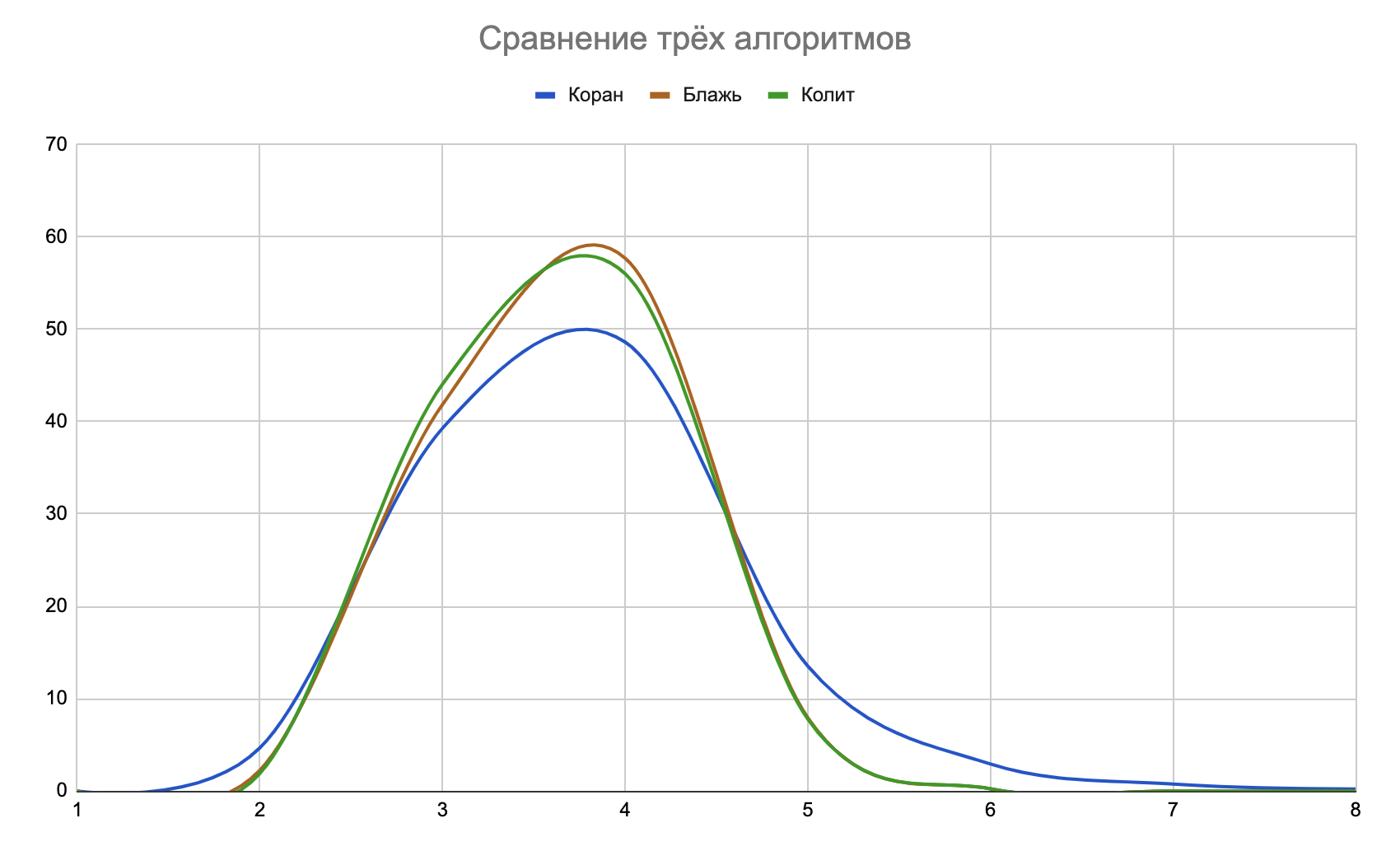
Среднее число шагов получилось выше, чем у частотных алгоритмов «Серна», «Стена» и «Норка». Но это не потому, что я играю лучше, чем программа, которая знает все слова, а потому, что в реальной игре короче словарь. Из-за этого, например, когда я называю слово, которое «Словль» не знает, он не засчитывает эту попытку. Я получаю информацию бесплатно и хожу по-другому.

Тем не менее вот все семь алгоритмов на одном графике:

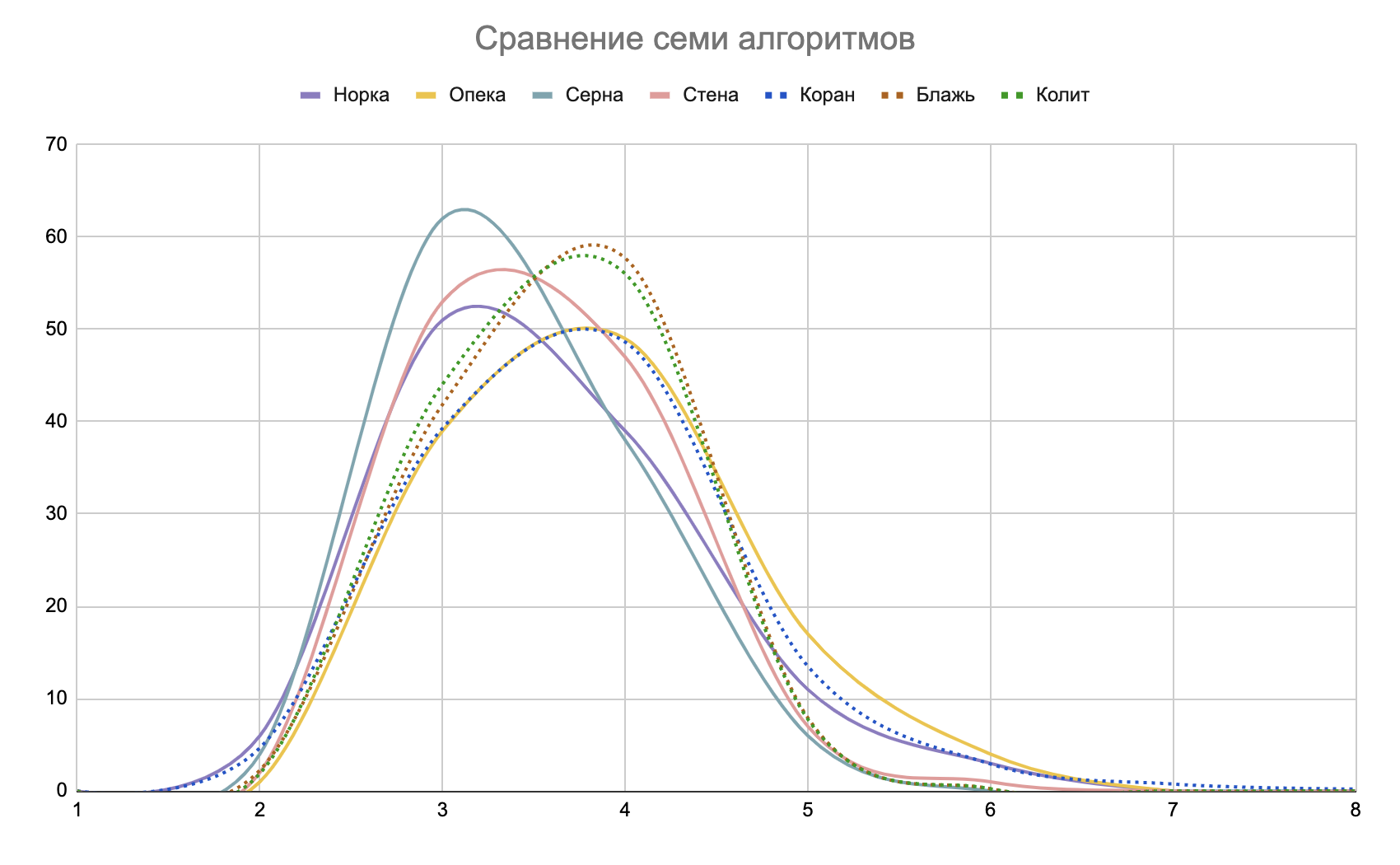
Поддавки

Теперь представим, что моя цель — сделать как можно больше ходов, но при этом не выиграть. Результат сильно зависит от ограничений на ходы.

Если я буду всё время ходить одним и тем же словом, я либо угадаю секрет первым же ходом, либо буду играть вечно.

Если запретить мне повторять ходы, то я постараюсь вычислить секрет, но при этом не назвать его. Если я не угадал секрет с первого хода, дальше я буду ходить только теми словами, которые заведомо отличаются от секрета хотя бы одной буквой или их расположением. После того как я вычислю секрет, я буду ходить всеми остальными словами и моя игра будет длиться столько ходов, на сколько пересекаются мой внутренний словарь и словарь игры.

Если разрешить мне ходить только теми словами, которые удовлетворяют всем известным к этому ходу ограничениям, то я буду делать ходы допустимыми словами с наименьшей ожидаемой информативностью, начиная со слова ИЧИГИ＊. В этом случае я закончу игру за ~6,134 ходов в среднем. То есть даже стараясь проиграть, я буду выигрывать в половине раундов.

Толкования некоторых слов